The goal of tout is to optimise the design of three-outcome clinical trials by determining their sample size and progression criteria.
Installation
Install the released version of tout from CRAN:
install.packages("tout")Or you can install the development version of tout from GitHub with:
# install.packages("devtools")
devtools::install_github("DTWilson/tout")Example
Consider a pilot trial which will measure the proportion of patients, in the intervention arm, who adhere to the intervention. We want to use this estimate of the probability of adherence (denoted ) in a statistical test with three possible outcomes: stop, go, or pause (where a pause outcome allows us to make the progression decision outwith the testing framework, based on other information and/or stakeholders).
Let the null and alternative hypotheses be and , and suppose we wish to control error rates at and . We can find the smallest possible design satisfying these constraints using the tout_design() function:
library(tout)
design <- tout_design(rho_0 = 0.5, rho_1 = 0.7, alpha_nom = 0.05, beta_nom = 0.2, gamma_nom = 0.6)
design
#> Three-outcome design
#>
#> Sample size: 57
#> Decision thresholds: 33 38
#>
#> alpha = 0.04808966
#> beta = 0.186012
#> gamma = 0.5433195
#>
#> Hypotheses: 0.5 (null), 0.7 (alternative)
#> Modification effect range: 0 0
#> Error probability following an intermediate result: 0.5 0.5Plotting the returned object gives an illustration of the sampling distribution of the estimated adherence probability under each hypothesis, alongside the optimal progression criteria and the decisions they will lead to:
plot(design)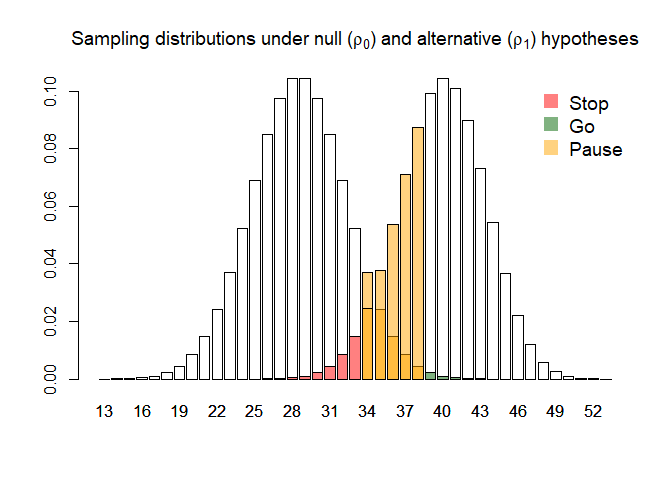
The same function can be used when we anticipate making some adjustments following a pause outcome (see the tau argument); when assuming particular probabilities of making correct decisions following a pause outcome (see the eta argument); and when the outcome is continuous rather than binary (see the sigma argument). Further details can be found in the vignette and in the associated manuscript.
