Skip to contents

Three-outcome clinical trial design (tout)

Source: vignettes/tout.Rmd
tout.Rmd

Introduction

Early phase clinical trials typically employ a hypothesis test as their primary analysis, with this test having two possible outcomes: we will either go to the next stage of evaluation (e.g. a large phase III trial), or we will stop development. In a testing framework these decisions correspond with the rejection of the null hypothesis, or the failure to reject it, respectively.

Some authors have suggested that phase II drug trials can extend this approach to allow for a third intermediate outcome, where we pause if we observe data that is not so bad as to warrant an immediate stop, nor so good as to warrant an immediate go. A similar approach is very common in pilot trials of complex interventions. In both settings, the mechanics are the same: we compute an estimate ρ̂\hat{\rho} of the parameter of interest, ρ\rho, and compare it against two thresholds, x0x_0 and x1x_1, such that

Decision={go if ρ̂≥x1pause if x0<ρ̂<x1stop if ρ̂<x0.\begin{equation}\label{eqn:three_outcome} \text{Decision} = \begin{cases} \text{go} & \text{ if } \hat{\rho} \geq x_1 \\ \text{pause} & \text{ if } x_0 < \hat{\rho} < x_1 \\ \text{stop} & \text{ if } \hat{\rho} < x_0. \\ \end{cases} \end{equation}

The tout package lets us determine optimal values for the decision thresholds x0x_0 and x1x_1 and the sample size nn. In particular, it will find the smallest possible trial which will satisfy constraints on the following three operating characteristics:

  • α\alpha, the probability of proceeding to the main trial when ρ≤ρ0\rho \leq \rho_0;
  • β\beta, the probability of not proceeding to the main trial when ρ≥ρ1\rho \geq \rho_1; and
  • γ\gamma, the probability of making an immediate stop or go decision when ρ=(ρ0+ρ1)/2\rho = (\rho_0 + \rho_1)/2.

A simple example

Suppose the parameter of interest, ρ\rho, is the probability of adherence in the intervention arm of a pilot trial. Suppose further that our null and alternative hypotheses are ρ0=0.5\rho_0 = 0.5 and ρ1=0.7\rho_1 = 0.7, respectively. Using typical type I and II error constraints, α≤0.05\alpha \leq 0.05 and β≤0.2\beta \leq 0.2, we can find the smallest design that will ensure a probability of at least 1−γ=0.51 - \gamma = 0.5 that we will obtain a pause decision if the true parameter value is midway between the null and alternative hypotheses:

design <- tout_design(rho_0 = 0.5, rho_1 = 0.7, alpha_nom = 0.05, beta_nom  = 0.2, gamma_nom = 0.5)

design
#> Three-outcome design
#> 
#> Sample size: 66 
#> Decision thresholds: 38 44 
#> 
#> alpha = 0.04488955 
#> beta = 0.1703036 
#> gamma = 0.496394 
#> 
#> Hypotheses: 0.5 (null), 0.7 (alternative)
#> Modification effect range: 0 0 
#> Error probability following an intermediate result: 0.5 0.5

We can visualise the sampling distribution of the test statistic under each hypothesis, highlighting the decisions which will be made:

plot(design)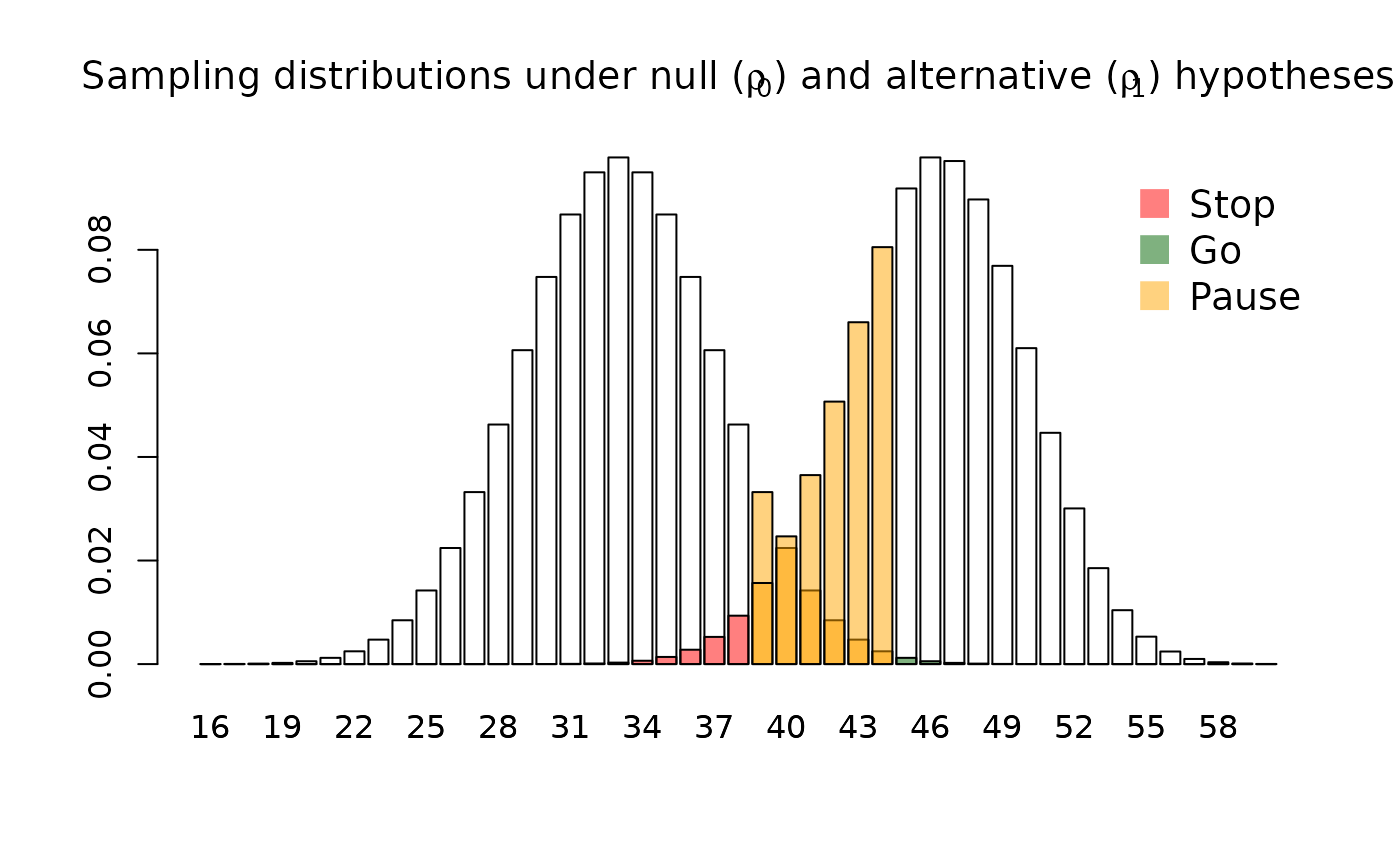

Making decisions following a pause outcome

The testing framework employed in tout acknowledges that a final stop/go decision must be made following a pause outcome, and factors this into the calculation of error rates. This requires an assumption about how well such decisions will be made; in particular, we must estimate the probabilities that we will incorrectly go when ρ≤ρ0\rho \leq \rho_0 (denoted η0\eta_0), and that we will incorrectly stop when ρ≥ρ1\rho \geq \rho_1 (denoted η1\eta_1). By default, tout_design() assumes that η0=η1=0.5\eta_0 = \eta_1 = 0.5, but we can change these if we wish:

design <- tout_design(rho_0 = 0.5, rho_1 = 0.7, alpha_nom = 0.05, beta_nom  = 0.2, gamma_nom = 0.5, eta_0 = 0.3, eta_1 = 0.4)

design
#> Three-outcome design
#> 
#> Sample size: 46 
#> Decision thresholds: 26 31 
#> 
#> alpha = 0.0492724 
#> beta = 0.1830351 
#> gamma = 0.4863821 
#> 
#> Hypotheses: 0.5 (null), 0.7 (alternative)
#> Modification effect range: 0 0 
#> Error probability following an intermediate result: 0.3 0.4

Making adjustments following a pause outcome

We often anticipate making some adjustments to the intervention and/or the trial design following a pause outcome, in an attempt to improve the parameter of interest and ensure the subsequent trial is successful. We can incorporate this in tout if we can specify an interval for the effect of this modification τ∈[τmin,τmax]\tau \in [\tau_{min}, \tau_{max}]. For example, suppose we anticipate an improvement in adherence in the range of τ∈[0.01,0.05]\tau \in [0.01, 0.05]. The optimal design is then

design <- tout_design(rho_0 = 0.5, rho_1 = 0.7, alpha_nom = 0.05, beta_nom  = 0.2, gamma_nom = 0.5, tau = c(0.01, 0.05))

design
#> Three-outcome design
#> 
#> Sample size: 100 
#> Decision thresholds: 55 63 
#> 
#> alpha = 0.04924659 
#> beta = 0.1988391 
#> gamma = 0.4732802 
#> 
#> Hypotheses: 0.5 (null), 0.7 (alternative)
#> Modification effect range: 0.01 0.05 
#> Error probability following an intermediate result: 0.5 0.5

Designs for continuous endpoints

By default, tout_design() assumes a binary endpoint. We can find designs for continuous endpoints if we supply the (assumed known) standard deviation of the outcome via the sigma argument. For example,

design <- tout_design(rho_0 = 2, rho_1 = 5, alpha_nom = 0.05, beta_nom  = 0.2, gamma_nom = 0.5, sigma = 7, tau = c(1, 2), max_n = 500)

design
#> Three-outcome design
#> 
#> Sample size: 179 
#> Decision thresholds: -0.6286741 1.644913 
#> 
#> alpha = 0.05 
#> beta = 0.2002572 
#> gamma = 0.3147751 
#> 
#> Hypotheses: 2 (null), 5 (alternative)
#> Standard deviation: 7 
#> Modification effect range: 1 2 
#> Error probability following an intermediate result: 0.5 0.5

Note that the decision thresholds are given on the scale of the z-statistic.

Further details

For the case of a binary endpoint, the three error rates are formally defined as:

α=max[Pr(x1<ρ̂|ρ=ρ0),ηPr(x0<ρ̂≤x1|ρ=ρ0−τmin)+Pr(x1<ρ̂|ρ=ρ0−τmin)]β=Pr(ρ̂≤x0|ρ=ρ1−τmax)+ηPr(x0<ρ̂≤x1|ρ=ρ1−τmax)γ=Pr(ρ̂≤x0|ρ=[ρ0+ρ1−τmin−τmax]/2)+Pr(x1<ρ̂|ρ=[ρ0+ρ1−τmin−τmax]/2). \begin{align} \alpha =& \max \big[ \Pr(x_1 < \hat{\rho} ~|~ \rho = \rho_0), ~\eta \Pr(x_0 < \hat{\rho} \leq x_1 ~|~ \rho = \rho_0 - \tau_{min}) \nonumber \\ &+ \Pr(x_1 < \hat{\rho} ~|~ \rho = \rho_0 - \tau_{min}) \big] \\ \beta =& \Pr(\hat{\rho} \leq x_0 ~|~ \rho = \rho_1 - \tau_{max}) + \eta \Pr(x_0 < \hat{\rho} \leq x_1 ~|~ \rho = \rho_1 - \tau_{max}) \\ \gamma =& \Pr(\hat{\rho} \leq x_0 ~|~ \rho = [\rho_0 + \rho_1 - \tau_{min} - \tau_{max}]/2) \\ &+ \Pr(x_1 < \hat{\rho} ~|~ \rho = [\rho_0 + \rho_1 - \tau_{min} - \tau_{max}]/2). \end{align}

Derivations of these are given in the associated manuscript. The case of continuous endpoints follows, now considering the test statistic to be a z-statistic with distribution

Z∼N(ρ−ρ0σ2/n,1). Z \sim N \left( \frac{\rho - \rho_0}{\sqrt{\sigma^2/n}}, 1 \right).

Given any nn and x1x_1, the x0x_0 corresponding to the nominal constraint on α\alpha can be found exactly. The optimal x1x_1 is determined numerically (using an exhaustive search in the binary case and optimize() in the continuous case) with respect to the nominal constraint on β\beta. Finally, a bisection search is used to find the lowest nn which satisfies the nominal constraint on γ\gamma.

References